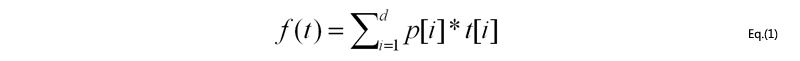|
Abstract
A top-k query returns k tuples with the highest (or the lowest) scores from a relation. Layer-ordering methods are well-known studies that process top-k queries effectively. These methods construct a database as a single list of layers. Here, the i-th layer has the objects that can be the top-i object. Thus, these methods answer top-k queries by reading at most k layers. Query performance, however, is poor when the number of objects in each layer (simply, the layer size) is large. In order to reduce the layer size, in this project, we will investigate the notion of partitioning layers, which constructs a database as multiple sublayer lists instead of a single layer list.
Project description
A top-k(ranked) query returns k tuples with the highest (or the lowest) scores in a relation [LCI+05]. A score function is generally in the form of a linearly weighted sum as shown in Eq.(1) [HKP01]. Here, p[i] and t[i] denote the weight and the value of the i-th attribute of a tuple t, respectively. The d-dimensional vector that has p[i] as the i-th element is called the preference vector [HKP01], where d denotes the number of attributes of t.
Top-k queries are widely used in a number of applications that need to find top-k results through ranking. For example, ranking colleges or ordering houses listed for sale are applications of top-k queries. Colleges are represented by a relation that has numerical attributes such as the assessment of faculty resources, school fee, and percentage of employment. Houses are represented by a relation that has numerical attributes such as the cost of housing, number of bedrooms, and area. Users search for the k colleges or houses with the highest scores according to their own preference vector [CBC+00, HKP01, XCH06].
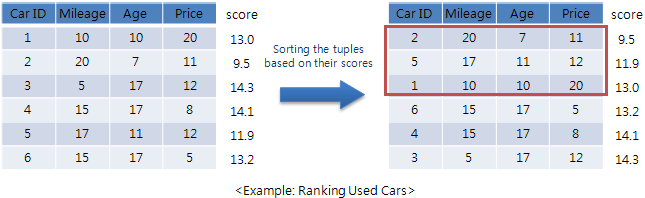
To process a top-k query, a naive method would calculate the score of each tuple according to the score function, and then, finds the top k tuples by sorting the tuples based on their scores. This method, however, is not appropriate for a query with a relatively small value of k over large databases because it incurs a significant overhead by reading even those tuples that cannot possibly be the results [XCH06].
Layer-ordering methods are well-known in that they process top-k queries effectively by accessing only a subset of the database instead of unnecessarily accessing the entire one [CBC+00, XCH06]. Layer-ordering methods construct the first layer with the objects that can be the top-1 object among the entire set of objects and construct the second layer with the objects that can be the top-2 object among the set of the remaining objects (i.e., objects excluding the objects in the first layer). By repeatedly preprocessing all the objects in the same manner, they construct a list of consecutive layers (simply, a layer list). The layer-ordering methods have two advantages: 1) storage overhead is negligible [CBC+00], and 2) query performance is not very sensitive to the preference vector of a score function given by the query [XCH06]. Nevertheless, it also has a serious disadvantage: when the number of objects in each layer (simply, the layer size) is large, these methods have bad query performance because many unnecessary objects have to be read to process the query [HKP01].
In this project, we will investigate a new layer-ordering method that reduces the layer size in order to improve query performance. First, we will propose the notion of the convex skyline, which is a combination of the convex hull [BKO+00] and the skyline [BKS01], in constructing layer lists. Using the convex skyline reduces the sizes of layers compared with using the convex hull or the skyline. Second, we will investigate the notion of partitioning layers, which constructs a database as multiple sublayer lists instead of a single layer list in order to further reduce the layer size. Finally, we will perform extensive experiments using synthetic and real data sets in order to evaluate the query performance advantage of our methods.
Organization
- Responsible Person
- Research Assistant
References
- [BKO+00] Berg, M., Kreveld, M., Overmars, M., and Schwarzkopf, O., Computational Geometry: Algorithms and Applications, 2nd ed., Springer-Verlag, 2000.
- [BKS01] Borzsonyi, S., Kossmann, D., and Stocker, K., "The Skyline Operator," In Proc. 17th Int'l Conf. on Data Engineering (ICDE), pp.421-430, Heidelberg, Germany, Apr. 2001.
- [CBC+00] Chang, Y. C., Bergman, L., and Castelli, V., "The Onion Technique: Indexing for Linear Optimization Queries," In Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp.391-402, Dallas, Texas, May 2000.
- [HKP01] Hristidis, V., Koudas, N., and Papakonstantinou, Y., "PREFER: A System for the Efficient Execution of Multiparametric Ranked Queries," In Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp.259-270, Santa Barbara, California, May 2001.
- [LCI+05] Li, C., Chang, K. C.-C., Ilyas, I. F., and Song, S., "RankSQL: Query Algebra and Optimization for Relational Top-k Queries," In Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp.131-142, Baltimore, Maryland, June 2005.
- [XCH06] Xin, D., Chen, C., and Han, J., "Towards Robust Indexing for Ranked Queries," In Proc. 32nd Int'l Conf. on Very Large Data Bases (VLDB), pp.235-246, Seoul, Korea, Sept. 2006.
|